Notions statistiques élémentaires
Le travail sur des données chiffrées nécessite quelques outils pour les "faire parler", car les longues séries de chiffres seules ne livrent pas d’information, il faut recourir à des indices représentatifs.
La moyenne arithmétique
La plus connue des formules : moyenne = somme de toutes les valeurs / nombre de valeurs
Simple, utile, mais aussi trompeuse ! Une moyenne n’est réellement significative que sur un grand nombre de valeurs, une moyenne est représentative de l’ensemble mais reste la valeur centrale. Pour en savoir plus, il faut connaître la répartition des valeurs autour de la moyenne, comment elles se distribuent.
L’étendue
L’étendue est l’écart entre la plus grande et la plus petite valeur de la série.
Si une série (une distribution) a pour valeur Max = 95 et pour min = 37, l’étendue E = 95 - 37 = 58
L’étendue permet de dire comment les valeurs se situent autour de la moyenne,
une étendue faible traduira le fait que les valeurs se groupent très près de la
moyenne, alors qu’une étendue forte, montrera une forte dispersion des valeurs.
Les moyennes seules ne
permettent pas de comparer deux phénomènes.
La médiane
La médiane est la valeur qui partage l’effectif (le nombre de valeurs) en deux parties égales : il y a 50% des valeurs sous la médiane et 50% au-dessus.
On peut déduire des 3 valeurs :
L’écart-type
L’écart-type, souvent appelé "déviation standard" et
noté s (sigma) permet de mesurer les dispersions des
données par rapport à la valeur centrale, qui est souvent la moyenne.
Sa formule est :
Ecart-type = 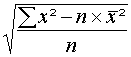
Indice de dispersion
L’écart-type a une propriété remarquable : 2s couvrent 68% de l’étendue, 4s en couvrent 96% et 6s couvrent 99.7% soit la quasi totalité de l’étendue.
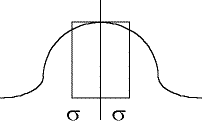
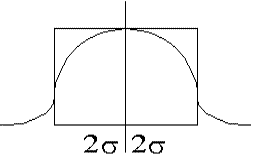
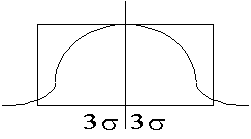
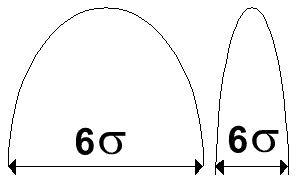
Plus un écart-type est grand, plus grande est la dispersion (courbe applatie à base large), plus il est faible, plus la dispersion est faible (courbe pointue à petite base).
On trouve souvent l’appellation " déviation standard " notée s (sigma). Pour un grand nombre d’échantillons, les résultats sont sensiblement les mêmes.Calcul de l’écart-type " à la main "
Pour n données, calculer le carré de chaque donnée, à la fin faire le total des carrés.
Appliquer la formule : (total des carrés - n x moyenne au carré) / n
On obtient ainsi la " variance ", qui est le carré de
l’écart-type, donc :
racine carrée du résultat précédent = écart-type.
Offert par
© Christian HOHMANN
