Quel ordre de passage assure le temps de production total le plus court ?

---

Solution : P1 P2 P3, Représentée selon un diagramme de Gantt :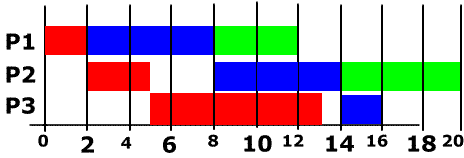

Au moment initial t0, P1 commence sur M1 qui le traitera en 2 unités de temps, avant de traiter P2 puis P3.
M1 aura fini en t13, comme le tableau le montrait (total M1).

M2 traite la pièce P1 dès que M1 la libère, puis P2 et P3.
Ni M1 ni M2 ne subissent d'attente.

M3 subit une attente de 2 unités de temps, en attendant que P2 soit achevée sur M2.
P2 et P3 attendent leur tour devant M1 puis M2.
Cependant, cette combinaison reste la meilleure globalement, tout autre combinaison dépassant t20.

Comment arrive-t-on au résultat optimal ?

Vous pouvez essayer une méthode intuitive en vous aidant de barres de LEGO ^® de couleurs et dimensions différentes, par exemple.

Quand vous en aurez assez, essayez ceci :

Algorithme de Johnson

Déterminer le produit P ayant le temps de process M1 ou M3 le plus court .

• si M1 alors P doit commencer sur ce process,
• si M3 alors P doit finir sur ce process,

Eliminer P de la liste et recommencer la recherche sur les P restants, et ainsi de suite.

Exemple 2

Six produits P1...P6 sont à produire. Il faut passer dans l'ordre sur M1,M2 et M3.
Chaque produit doit être totalement fini sur Mi avant de passer sur Mi+1.
Les temps de cycle sont donnés par le tableau :

Séquencement :

P6 doit terminer sur M3, puis 4 cas possibles:

• P1 doit commencer sur M1 (ou terminer sur M3)
• P2 doit commencer sur M1
• P5 doit terminer sur M3
• P3 doit terminer sur M3

Nous obtenons 4 combinaisons possibles, Laquelle est la meilleure ?

• 1) P1 P2 P4 P3 P5 P6 date de fin 36
• 2) P2 P1 P4 P3 P5 P6 date de fin 32
• 3) P2 P4 P3 P5 P1 P6 date de fin 36
• 4) P2 P4 P3 P1 P5 P6 date de fin 32

(Calcul des dates de fin, par diagramme ou calcul)

Les solutions 2) et 4) sont les meilleures.

L’algorithme présente l’inconvénient, en cas de temps opératoires égaux, de devoir explorer toutes les solutions, ou d’en choisir une arbitrairement. Or entre les quatre solutions, équivalentes 2 à 2, il ya une différence de 4 unités de temps, ce qui n’est pas négligeable !

L'Algorithme de Johnson généralisé

(N Produits passant sur M machines)

Calculer pour chaque produit x = somme des n-1 premiers process (dernier process exclu)

Calculer pour chaque produit y = somme des n-1 derniers process (premier process exclu)

Calculer pour chaque produit k = x / y

Le séquencement sera celui des produits triés selon l’ordre croissant de leurs coefficient k.

En reprenant l’exemple 1 :

	M1	M2	M3	x	y	k
P1	2	6	4	8	10	0.80
P2	3	6	6	9	12	0.75
P3	8	2	0	10	2	5.00

Solution : P2 P1 P3, date de fin = 21

---

En reprenant l’exemple 2 :

	M1	M2	M3	x	y	k
P1	2	6	2	8	8	1.0
P2	2	6	6	8	12	0.66
P3	8	2	6	10	8	1.25
P4	6	2	8	8	10	0.8
P5	6	6	2	12	8	1.5
P6	6	3	0	9	3	3.0

Solution : P2 P4 P1 P3 P5 P6, date de fin = 33

Dans les exemples 1 et 2 repris par l'algorithme généralisé, les solutions trouvées sont équivalentes (mais non optimales) aux meilleures selon l’autre méthode, avec une économie de temps et une simplification des calculs.

---

Calculs des dates de début, date de fin et marges

Posons comme origine des temps to le début du cycle P1 sur M1.

Par convention, nous adopterons la notation :

pour date de début du produit sur le process,

pour date de fin du produit sur le process, et étant entendu que l’indice produit est celui après tri.

Occupation de M1 = somme des temps cycle P1 à P6 sur M1, soit 30 unités.
Les produits peuvent se suivre sans temps mort. Date de fin sur M1 = 30 = Tf¹₆

Occupation de M2 : le travail de P2 sur M2 ne peut commencer que quand P2 est achevée sur M1, soit à t=2, P4 ne peut commencer qu’après la fin de P2, soit à t=8, P1 à t=10 etc...

On peut construire le tableau suivant qui regroupe toutes les informations, en utilisant un algorithme du type :

Tant que n

n suivant

		M1				M2				M3
	d	Td	Tf	c	d	Td	Tf	c	d	Td	Tf	c
P2	2	0	2	0	6	2	8	0	6	8	14	0
P4	6	2	8	0	2	8	10	0	8	14	22	0
P1	2	8	10	0	6	10	16	0	2	22	24	0
P3	8	10	18	0	2	18	20	2	6	24	30	0
P5	6	18	24	0	6	24	30	4	2	30	32	0
P6	6	24	30	0	3	30	33	0	0	32	32	0

d = durée, c = contrainte

Une contrainte est le temps d’attente nécessaire à l’achèvement d’un produit sur un process avant de passer ce produit sur le process suivant (libre), ou de passer le produit suivant déjà prêt sur ce process.

Cette attente forcée peut être considérée comme une marge : on peut retarder un produit de la valeur de la contrainte qu’il subit sans que cela change la date de fin.

---

Calcul de la marge

Calcul de la marge :

---

Utilisation possible des marges

P3 peut démarrer sur M2 à t=18 au plus tôt et finit à t=20.
Le prochain produit (P5) ne sera disponible pour M2 qu’à t=24.
De plus, sur M3, on ne peut commencer P3 qu’à t=24. Cette attente forcée de P3 peut être convertie en marge, en considérant date de début au plus tôt P3 sur M2 = 18, date de début au plus tard = date de début au plus tôt + marge (18+4=22).
En commençant P3 sur M2 à t=22, on ne modifie en rien à la suite des opérations et aux dates de fin.

Gains : l’arrêt de M2 est allongé, cela permet de rationnaliser l’emploi de cette machine, de faire des maintenances préventives, économiser l'énergie ou encore de mieux répartir la main d'oeuvre, qui peut être affectée rationnellement.